이 포스팅은 알고리즘 문제 해결 전략 책을 공부한 후 작성한 것입니다.

▶ 1편 알고리즘의 시간 복잡도 분석 (1) - 시간 복잡도와 수행 시간 보고 오기



점근적 시간 표기: 대문자 O 표기법(Big-O Notation)

  • O 표기법은 주어진 함수에서 가장 빨리 증가하는 항만을 남긴 채 나머지를 다 버리는 표기법
    • 시간 복잡도는 계산하기 힘들다는 문제점이 있음
      • 모호한 필요 명령어의 수, 복잡한 알고리즘에서의 명령 수 계산 등
      • 따라서 가장 깊이 중첩된 반복문의 개수만 고려했던 것처럼 전체 수행 시간에 큰 영향을 미치지 않는 상수 부분은 무시하고 반복문의 반복 수만 고려하게 되는 것
    • 예시
      • 어떤 알고리즘의 수행 시간이 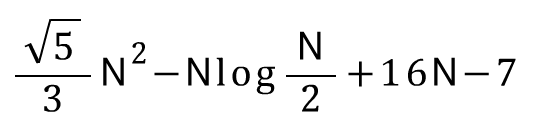이라고 하면, 네 개의 항 중 N이 가장 빨리 증가하는 항은 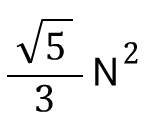이므로 상수를 떼어내면 N^2임. 그래서 이 알고리즘의 수행 시간을 O(N^2)라고 표기
  • 예제 알고리즘의 반복문 수행 횟수와 시간 복잡도의 O 표기
알고리즘 반복문의 수행 횟수 O 표기
이동 평균 구하기 N O(N)
이진 탐색 logN O(logN)
집합 덮개 NM2^M O(NM2^M)
  • 알고리즘 입력의 크기가 두 개 이상의 변수로 표현될 때는 그 중 가장 빨리 증가하는 항들만을 떼 놓고 나머지를 버림
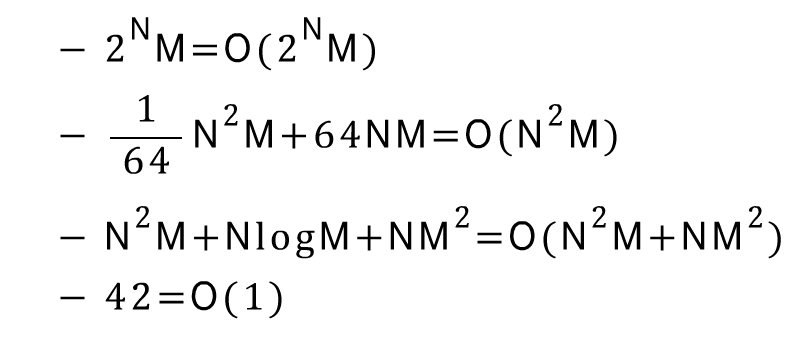
    • 예시

O 표기법의 의미

  • O 표기법은 계산하기 간편하고 알아보기 쉬움
  • 대략적으로 함수의 상한을 나타냄
    • 아주 큰 N0과 C(N0, C>0)를 적절히 선택하면 N0<=N인 모든 N에 대해 |f(N)|<= Cxlog(N)|이 참이 되도록 할 수 있음
      • 예를 들어 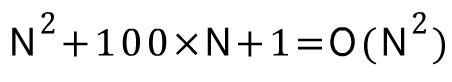라고 표기하는 시간 복잡도가 있을 때
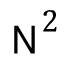      • 는 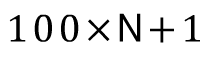보다 작지만 이 중에서 가장 빨리 증가하는 항
      • N이 엄청나게 커지면 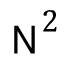과 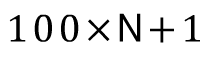사이에는 그다지 큰 차이가 없게 됨
      • 이 때 적절한 상수 C를 선택해서 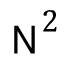에 곱해주면 항상 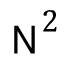이 더 크다고 할 수 있음 (C와 N은 마음대로 결정할 수 있음)
        • 예: C=2, N0=1000이라고 하면 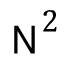이 2백만으로 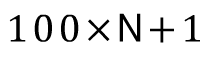보다 훨씬 크게 됨
  • O 표기법은 각 경우의 수행 시간을 간단히 나타내는 표기법일 뿐, 특별히 최악의 수행 시간과 관련이 있는 것은 아님
    • 예를 들어 퀵 정렬의 최악의 수행 시간을 분석해 보면 최고차항이 N^2이므로 시간 복잡도는 O(N^2)임
    • 그러나 평균 수행 시간을 계산해 보면 최고차항이 NlogN로, 평균 시간 복잡도는 최악의 경우와 달리 O(NlogN)

시간 복잡도 분석 연습

선택 정렬

모든 i에 대해 A[i…N-1]에서 가장 작은 원소를 찾은 뒤, 이것을 A[i]에 넣는 것을 반복

def selectionSort(A):
    for i in range(len(A)):
        minIndex = i
        for j in range(len(A)):
            if A[minIndex] > A[j]:
                minIndex = j
        A[i], A[minIndex] = A[minIndex], A[i]
  • for문 내부의 if문의 수행 횟수를 보면 i=0일 때 N-1번, i=1일 때 N-2번, i=N-1일 때 0번
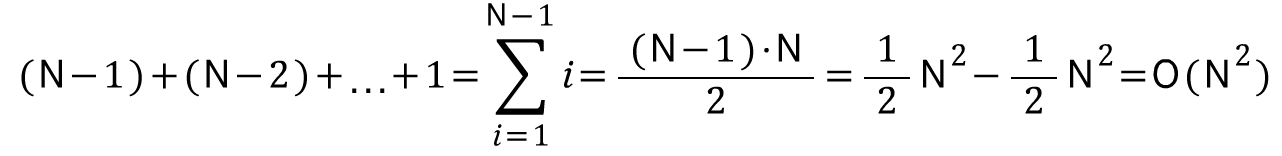
  • 혹은 최대 O(N)번 실행되는 for문이 두 개 겹쳐 있기 때문에 최종 시간 복잡도는 O(N^2)라고 계산해도 됨
  • 선택 정렬의 시간 복잡도는 A[]에 포함된 원소와는 상관 없이 A[]의 크기 N에 의해서만 결정되기 때문에 최악의 경우와 최선의 경우에 시간 복잡도가 같음

삽입 정렬

전체 배열 중 정렬되어 있는 부분 배열에 새 원소를 끼워넣는 일을 반복적으로 수행

def insertionSort(A):
    for i in range(len(A)):
        j = i
        while (j > 0 and A[j-1] > A[j]):
            A[j-1], A[j] = A[j], A[j-1]
            j -= 1
  • 삽입을 위해 A[i]에 있던 값을 하나씩 앞으로 옮기기 위해 j에 대한 while문 사용
  • A[j]에 있는 숫자보다 작은 숫자를 만날 때까지 A[j]를 앞으로 옮겨 감
  • while문의 수행 횟수는 처음에 A[j]에 위치한 값에 따라 달라지므로 선택 정렬과 달리 입력 배열의 초기 순서에 따라 비교의 횟수가 달라지는 특성을 가짐
    • 최선의 경우: 이미 정렬된 배열이 주어지는 경우 = while문 작동 안 함, for문에 대한 시간 복잡도만 필요하므로 배열의 크기가 중요 = 선형 시간 O(N)
    • 최악의 경우: 역순으로 정렬된 배열이 주어지는 경우 = while문 시간 복잡도 O(N), 전체 시간 복잡도 O(N^2)