데이터와 표본분포 - (1) 표본추출과 편향
by Yurim Koo
표본추출의 중요성
- 빅데이터 시대가 되면서 더는 표본추출이 필요 없을 것이라고 생각하는 사람이 증가
- 그러나 데이터의 질과 적합성을 일정 수준 이상으로 담보할 수 없으면서 데이터 크기만 늘어나는게 오늘날 상황
- 오히려 다양한 데이터를 효과적으로 다루고 데이터 편향을 최소화하기 위한 방법으로 표본추출의 중요성이 더욱 커짐
표본과 모집단
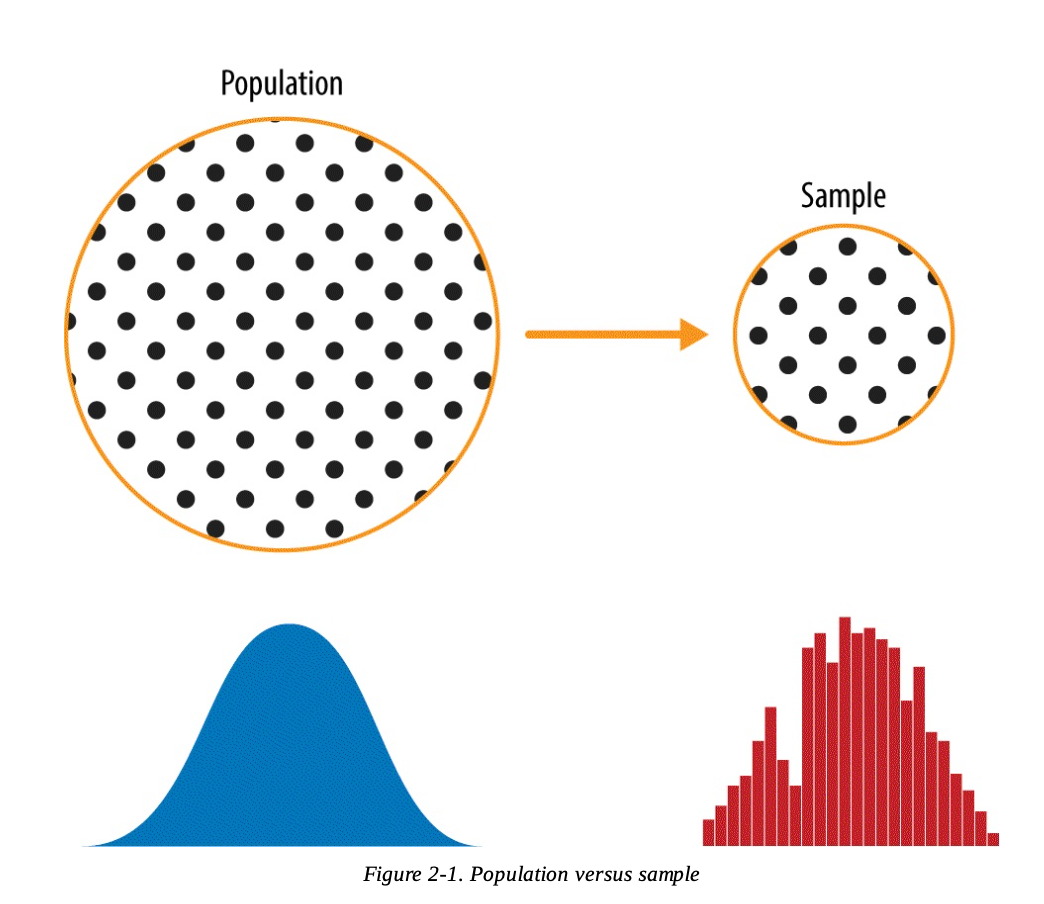
- 그림의 왼편은 미지의 분포를 따를 것으로 추정되는 모집단을 나타냄. 모집단은 때로 이론적인 가상의 집합을 의미하기도 함
- 오른편은 표본 데이터와 그를 통해 얻은 분포. 표본은 더 큰 데이터 집합(=모집단)으로부터 얻은 데이터의 부분집합
- 왼쪽에서 오른쪽을 얻어내는 것이 표본추출의 절차
- 전통적인 통계학에서는 강력한 가정에 기초한 이론을 통해 왼쪽의 모집단을 밝혀내는 데 초점을 맞춘데 비해, 현대 통계학에서는 이러한 가정이 더 이상 필요하지 않은 오른쪽에 대한 연구로 방향이 옮겨지기 시작
랜덤표본추출
- 랜덤표본추출은 대상이 되는 모집단 내의 선택 가능한 원소들을 무작위로 추출하는 과정
- 각 추첨에서 모든 원소는 동일한 확률로 뽑히게 되고, 그 결과 얻은 샘플을 단순랜덤표본이라고 지칭
- 추첨 후 다음번에도 중복 추출이 가능하도록 해당 샘플을 다시 모집단에 포함시키는 복원 추출과 한 번 뽑힌 원소는 추후 추첨에서 사용하지 않는 비복원추출로 표본을 얻을 수 있음
- 층화표본추출은 모집단을 여러 층으로 나누고 각 층에서 무작위로 샘플을 추출. 특정 층의 표본 수가 적다면 해당 층에 높은 가중치를 주는 표본추출을 통해 계층마다 동일한 표본크기를 얻을 수 있음
표본편향
- 샘플 기반의 추정이나 모델링에서 데이터 품질은 데이터의 양보다 중요
- 데이터 과학에서 데이터 품질이란 완결성, 형식의 일관성, 깨끗함 및 각 데이터 값의 정확성을 뜻함. 통계는 여기에 대표성이라는 개념을 추가함
- 표본편향은 원래 대표되도록 의도된 모집단으로부터 추출되지 않고 유의미한 비임의 방식으로 표본이 추출되는 현상
- 비임의 방식은 아무리 랜덤 표본이라고 해도, 어떤 표본도 모집단을 정확하게 대표할 수 없다는 것을 의미
- 모집단과 표본 사이의 차이가 유의미 할 만큼 크고, 첫 번째 표본과 동일한 방식으로 추출된 다른 샘플들에서도 이 차이가 계속될 것이라고 예상될 때 표본편향이 발생했다고 볼 수 있음
편향
- 통계적 편향은 측정 과정 혹은 표본추출 과정에서 발생하는 계통적인 오차를 의미
- 랜덤표본추출로 인한 오류와 편향에 따른 오류는 신중하게 구분해서 봐야 함
목표물에 총을 쏘는 과정을 생각해보자.
매번 목표물의 한가운데를 정확히 맞힌다는 것은 불가능하다.
한가운데에 정확히 한 발 맞히기도 힘들 것이다.
편향되지 않은 프로세스에도 오차가 있긴 하지만, 그것은 랜덤하며 어느 쪽으로 강하게 치우치는 경향이 없다.
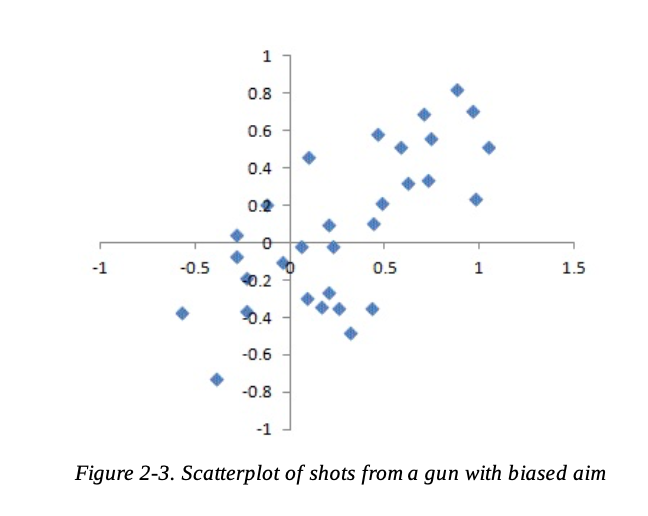
반면 편향된 조준사격의 경우 x방향과 y방향 모두에서 랜덤한 오차가 있고 편향도 있다. 탄착점이 오른쪽 위 사분면에 떨어지는 경향을 볼 수 있다. - 책 [데이터 과학을 위한 통계]
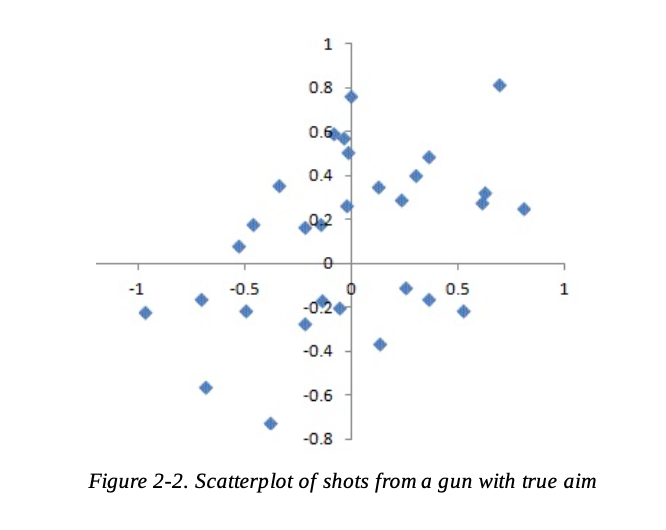
- (왼) 랜덤표본추출로 인한 오류: 오차가 랜덤하며 어느 쪽으로 강하게 치우치는 경향이 없음
- (오) 편향에 따른 오류: 랜덤한 오차도 존재하고 특정한 곳으로 치우치는 경향이 있음
참고자료
![[데이터 과학을 위한 통계]](/assets/img/data-and-sample-distribution/4.jpeg)
- 책 [데이터 과학을 위한 통계]
Subscribe via RSS
