데이터와 표본분포 - (2) 표본분포
by Yurim Koo
통계학에서의 표본분포
- 표본분포는 하나의 동일한 모집단에서 얻은 여러 샘플에 대한 표본통계량의 분포
- 고전 통계의 대부분은 (작은) 표본을 가지고 (매우 큰) 모집단을 추론하는 것과 관련
- 용어 정리
- 표본통계량(sample statistics): 더 큰 모집단에서 추출된 표본 데이터들로부터 얻은 측정 지표
- 데이터 분포(data distribution): 어떤 데이터 집합에서의 각 개별 값의 도수분포
- 표본분포(sample distribution): 여러 표본들 혹은 재표본들로부터 얻은 표본통계량의 도수분포
표본의 변동성 (sampling variability)
- 일반적으로 표본통계량으로 어떤 것을 추정하거나 통계 또는 머신러닝으로 무언가를 모델링하기 위해 표본을 추출
- 표본을 통해 추정하고 모델링을 하기 때문에 오류가 존재할 수 있고, 다른 표본을 뽑았다면 결과가 달라질 수 있음
- 흔히 데이터 분포라고 알려진 개별 데이터 포인트의 분포와 표본분포라고 알려진 표본통계량의 분포를 구별하는 것이 중요함
중심극한정리 (central limit theorem)
- 표본크기가 커질수록 표본분포가 정규분포를 따르는 경향
- 모집단이 정규분포가 아니더라도, 표본크기가 충분하고 데이터가 정규성을 크게 이탈하지 않는 경우, 여러 표본에서 추출한 평균은 종 모양의 정규곡선을 따름
- 평균과 같은 표본통계량의 분포는 데이터 자체의 분포보다 규칙적이고 종 모양일 가능성이 높음
- 표본이 클수록 표본통계량의 분포가 좁아짐
- 중심극한정리를 이용해 추론을 위한 표본분포에, 즉 신뢰구간이나 가설검정을 계산하는 데에 t 분포 같은 정규근사 공식을 사용할 수 있음
- 전통적인 통계에서는 중요성이 크지만, 대부분의 경우 부트스트랩을 사용할 수 있기 때문에 형식적인 가설검정이나 신뢰구간이 데이터 과학에서는 전통적인 통계학에서만큼 중요하지는 않음
표준오차 (standard error)
- 여러 표본들로부터 얻은 표본통계량의 변량 (개별 데이터 값들의 변량을 뜻하는 표준편차와 혼동하지 말 것)
- 표준오차는 통계에 대한 표본분포의 변동성을 한마디로 말해주는 단일 측정 지표
- 표본 값들의 표준편차 s와 표본크기 n을 기반으로 한 통계량을 이용하여 추정할 수 있음
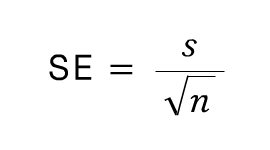
- 표본크기가 커지면 표준오차가 줄어듦
- 표준오차와 표본크기 사이의 관계를 때로는 n 제곱근의 법칙(square-root of n rule)이라고 함; 즉, 표준오차를 2배로 줄이려면 표본크기를 4배 증가시켜야 함
표준오차를 측정할 때 고려해야 할 사항
- 모집단에서 완전히 새로운 샘플들을 많이 수집한다.
- 각각의 새 샘플에 대해 통계량 (예: 평균) 을 계산한다.
- 2단계에서 얻은 통계량의 표준편차를 계산한다. 이것을 표준오차의 추정치로 사용한다.
- 실제로 표준오차를 추정하기 위해 새 샘플을 수집하는 접근 방식은 일반적으로 불가능하고 통계적으로도 낭비가 심함
- 새로운 샘플을 뽑을 필요가 없이 부트스트랩 재표본을 사용할 수 있음; 현대 통계에서 부트스트랩은 표준오차를 추정하는 표준 방법이 됨
- 부트스트랩은 사실상 모든 통계에 사용할 수 있으며 중심극한정리 또는 기타 분포 가정에 의존하지 않음
표준편차와 표준오차
- 표준편차: 개별 데이터 포인트의 변동성을 측정하는 지표
- 표준오차: 표본 측정 지표의 변동성을 측정하는 지표
- 두 지표는 다르므로 혼동하지 말 것
참고자료
![[데이터 과학을 위한 통계]](/assets/img/data-and-sample-distribution/4.jpeg)
- 책 [데이터 과학을 위한 통계]
Subscribe via RSS
